Willkommen zurück bei der Serie „Wieviel darf Wachstum kosten“! In Teil 1 hatte ich ein Modellunternehmen definiert, anhand dessen ich meine Rechnungen durchführen will. Wer den Artikel noch nicht gelesen hat: hier entlang!
Zur Erinnerung: Wir benutzen eine „Discounted Cashflow“-Methode (DCF). Wir berechnen also den fairen Wert eines Unternehmens anhand der Geldmenge, die es im Laufe seiner weiteren Existenz produziert.1Wir unterscheiden hier nicht zwischen Gewinn und Barmittelflüssen (Cashflows).
Für diese Geldmenge müssen wir eine Vorhersage treffen. In Teil 1 haben wir ein Modell definiert, das nur zwei Eingabewerte braucht: Eine Wachstumsrate, und die zugehörige Wachstumsdauer. Nach einer Phase konstanten Wachstums geht das Unternehmen in eine (ewige) Phase konstanten Gewinns über. Die Summe der abgezinsten Cashflows ist der faire Wert des Unternehmens.
Heute schreiten wir zur Anwendung und produzieren einige Ergebnisse – und zwar auf zwei verschiedene Arten.
- Wir können „vorwärts“ rechnen, also einfach Zahlen einsetzen und schauen, was herauskommt.
- Wir können aber auch rückwärts rechnen: Wir nehmen ein reales Unternehmen, setzen eine sinnvolle Wachstumsrate ein, und sehen, wie lange dieses Wachstum anhalten müsste, um den derzeitigen Marktpreis zu rechtfertigen.
Vorwärts rechnen – wie teuer darf Wachstum sein?
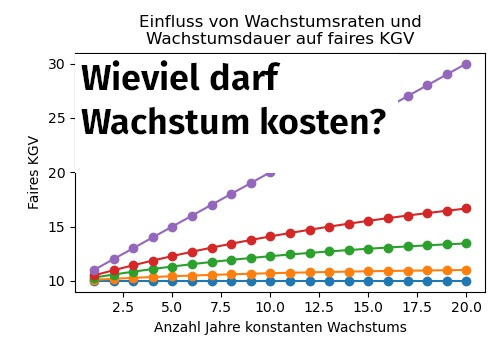
Los geht’s. Als erstes betrachten wir Anwachsraten bis maximal 10%, und wir nehmen (wie schon in früheren Artikeln) eine Discountrate von 10% an. Für jede Anwachsrate variieren wir die Dauer der Wachstumsphase. Daraus ergeben sich die in Abbildung 1 dargestellten Kurven:

Betrachten wir zunächst einmal die blaue Kurve, die zu 0% Wachstum gehört: Hier beträgt das faire Kurs-Gewinn-Verhältnis immer 10. Die Cashflows bleiben hier immer konstant, da die „Wachstumsphase” identisch zur Phase konstanten Cashflows ist. Wie im Artikel zur ewigen Rente beschrieben, ergibt sich das faire KGV in diesem Fall allein aus der gewählten Discountrate.
Geben wir ein kleines bisschen Wachstum hinzu: Bei 1% jährlichem Wachstum (orange Kurve) tut sich noch nicht viel: Erwarten wir, dass dies für 20 Jahre durchgehalten werden kann, so erhöht sich das faire KGV gerade einmal auf 11.
Interessanter wird es bei den höheren Wachstumsraten: Mit 5% Wachstum (rote Kurve) über 20 Jahre hinweg können wir ein KGV von ~17 als fair bezeichnen. Wird dasselbe Wachstum hingegen nur über 10 Jahre hinweg gehalten, wäre ein KGV von 14 fair. Da wir immer noch schneller abzinsen als das Unternehmen wächst, bringen die frühen Jahre hier einen größeren Zuschlag.
Bei 10% Wachstum (lila Kurve) zinsen wir genauso schnell ab, wie das Unternehmen wächst. Mit zunehmender Dauer der Wachstumsphase nimmt daher auch der faire Preis des Unternehmens linear zu. Für 10 Jahre Wachstum bei 10% jährlich dürfen wir daher ein KGV von 20 berappen. Für 20 Jahre Wachstum wäre bereits ein KGV von 30 fair.
An dieser Stelle schielen wir noch einmal zu Teil 1 dieses Artikels: Dort hatte ich unter anderem auch das Größenwachstum betrachtet, das ein Unternehmen während seiner Wachstumsphase durchläuft. 10% Wachstum über 20 Jahre, das entspricht knapp einem Faktor 7 Wachstum.
Wer also losstürmen will, um das nächste Unternehmen mit einem 30er KGV zu kaufen, könnte sich vorher fragen: Ist ein Wachstum um einen Faktor 7 über die nächsten 20 Jahre plausibel? Gibt es Beispiele von Unternehmen in einer ähnlichen Lage, die so etwas geschafft haben?
Wenn die Antworten „ja“ lauten, bzw. man bereit ist, das Risiko einzugehen: na dann los!
Gehen wir noch einen Schritt weiter und schauen uns die Anwachsraten jenseits von 10% an. In Abbildung 2 sind dieselben Berechnungen wie bisher gezeigt – allerdings bis hoch zu Anwachsraten von 100% jährlich. Achtung: Die y-Achse ist jetzt logarithmisch, denn das schnelle Wachstum hat Konsequenzen:
Der Unternehmensgewinn wächst jetzt schneller als wir abzinsen. Daher wächst das faire KGV ungefähr exponentiell mit der Dauer der Wachstumsphase.

Und die Ergebnisse sind beeindruckend:
Bereits 20% Wachstum (braune Kurve), über 10 Jahre durchgehalten, rechtfertigen ein KGV von 40. Wird dieses Wachstum sogar 20 Jahre gehalten, ginge sogar ein KGV von 110 noch in Ordnung. Das Größenwachstum der Firma betrüge dann einen Faktor 6 (10 Jahre), bzw. einen Faktor von knapp 40 (20 Jahre).
Bei einer Anwachsrate von 50% (grau) wäre ein KGV von 100 in Ordnung, wenn das Wachstum über 7 Jahre gehalten wird. Die Firma würde sich während dieser Zeit um etwa einen Faktor 18 vergrößern.
Schafft es eine Firma sogar, sich fünf Jahre lang jedes Jahr zu verdoppeln (gelbe Kurve), so wäre ein heutiges KGV von über 200 fair. Die Firma würde in dieser Zeit um etwa einen Faktor 30 wachsen.
Interessante Zahlen, werden einige nun sagen – aber wie soll mir das helfen, wenn man doch solch eine gloriose Zukunft nur selten vorhersehen kann?
Diesem Einwand muss man wohl mindestens teilweise stattgeben. Eine interessantere, und immer anwendbare (!) Variante dieser Rechnungen ist daher die, die ich im Folgenden beschreiben will.
Rückwärts rechnen – wieviel Wachstum ist eingepreist? Reale Beispiele
Die Idee ist angelehnt an das Buch „Expectations Investing“ von Mauboussin und Rappaport2Link zeigt auf die bald erscheinende Neuausgabe. Das Original ist bereits gut 20 Jahre alt.. Das Prinzip beruht darauf, die vom Marktpreis implizierten Annahmen über das Unternehmen zu verstehen, oder einfacher gesagt, die folgende Frage zu beantworten:
Wie muss sich das Unternehmen in Zukunft entwickeln, um den derzeitigen Preis zu rechtfertigen?
Eine ganz simple Variante dieser Berechnungen will ich hier zeigen. Und zwar gehen wir wie folgt vor: Wir greifen uns zwei Beispiele, sowie deren KGVs, und betrachten, wie stark und wie lange die Unternehmen wachsen müssten, um den derzeitigen Preis zu rechtfertigen.
Beispiel 1 – Apple
Im Artikel zur ewigen Rente hatte ich anhand des Beispieles Apple gezeigt, wie starkes Wachstum die Berechnung der ewigen Rente aushebelt. Jetzt beißen wir mit unserer neuen Methode nochmal kraftvoll in den Apfel. Wie gehen wir genau vor?
Wir nehmen die Wachstumsrate des Free Cash Flows von Apple seit 2017 (12,3% p.a.) und füttern diese in unser Unternehmensmodell. Das aktuelle KGV (13.09.2021) von Apple beträgt 29,2.
In Abb. 3 ist das faire KGV je nach Dauer der Wachstumsphase dargestellt, für die Wachstumsrate von Apple. Zur Orientierung zeigt die gepunktete Linie das tatsächliche KGV des Unternehmens. Wir können daran ablesen: Um den derzeitigen Preis von Apple unter unseren Annahmen zu rechtfertigen, muss das Wachstum der vergangenen vier Jahre sich noch mindestens 14 Jahre lang fortsetzen.

Der Vorteil bei dieser Methode: Wir müssen nicht raten, wie wohl das zukünftige Wachstum aussehen wird, sondern können untersuchen, wie viel Wachstum der Markt denn derzeit einpreist. Im Buch „Expectations Investing“ wird diese Methode noch stark verfeinert, so dass man z.B. auch die künftige Entwicklung der Gewinnmargen berücksichtigen kann.
Beispiel 2 – Tesla
Als zweites Beispiel wenden wir uns Tesla zu. Da Tesla noch nicht lange profitabel ist, nehmen wir das Umsatzwachstum seit 2016 zur Hand (45,7% p.a.) und nehmen an, dass das Unternehmen dieses Wachstum mit den derzeitigen Margen in Zukunft fortsetzen würde.
Eine Schätzung des Free Cash Flow für die nächsten 12 Monate liegt bei knapp $4 Mrd.3Quelle: TIKR. (kostenloser Einladungslink). Mit dieser Zahl bilden wir ein KGV von derzeit 183,2.4Diese Schätzung ist eher großzügig. Der Gewinn der letzten 12 Monate betrug $2,3 Mrd. Das tatsächliche KGV bezogen auf die letzten 12 Monate liegt derzeit bei 383,5.

In Abb. 4 ist die Abhängigkeit des fairen KGVs von der Wachstumsdauer dargestellt, zusammen mit dem derzeitigen KGV. Wir lesen wieder von der Grafik ab: Der derzeitige Preis der Tesla-Aktie beinhaltet die Annahme, dass das Unternehmen weiterhin mit 45,7% pro Jahr wächst, und zwar für weitere 9 Jahre.
Einen weiteren Schritt können wir noch vornehmen: In Teil 1 habe ich gezeigt, wie wir das angenommene Wachstum als Plausibilitätsprüfung einsetzen können. Wie stark würde das Unternehmen in dieser Zeit wachsen, und wie sinnvoll ist diese Zahl? Im vorliegenden Fall – 9 Jahre, 45,7% Wachstum – ergibt sich ein Wachstum um etwa einen Faktor 29. Ausgehend von 2020, müsste Teslas Umsatz dann gut $900 Mrd. betragen.
Zugegeben: Hier haben wir einige grobe Vereinfachungen vorgenommen, die man noch detaillierter überprüfen müsste, bevor man hier investiert oder nicht. Darf man z.B. annehmen, dass die Margen (in diesem Fall Free Cash Flow geteilt durch Umsatz) sich nicht ändern? Trotzdem konnte ich das Potential dieser Methode hoffentlich sichtbar machen.
Wie geht es jetzt weiter?
Wir haben noch einige offene Fragen: Zum Einen haben wir bis jetzt den fairen Preis als Summe der zukünftigen Cashflows berechnet. Darin steckt die verborgene Annahme, dass wir diese Cashflows auch zu 100% bekommen, sprich: wir müssten die alleinigen Besitzer des Unternehmens sein.
Was aber, wenn dem nicht so ist? Was, wenn das Unternehmen keine Dividende zahlt, und auch keine Aktienrückkäufe tätigt, wie im Falle von Tesla? Dann sind wir als Aktionäre komplett vom Wiederverkaufswert abhängig. Gelten dann andere Regeln? Wenn ja, welche?
Und schließlich: Gibt es eine nützliche Faustregel, mit der man den fairen Wert eines Unternehmens – auch wenn es schnell wächst – abschätzen kann?
Es bleibt also spannend. Brennen euch noch weitere Fragen unter den Nägeln? Lasst es mich wissen! Ansonsten: Stay tuned und bis bald!

Ein Gedanke zu „Wieviel darf Wachstum kosten? Teil 2: Beispielrechnungen.“